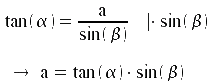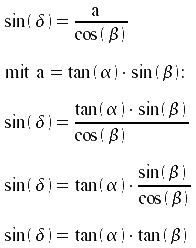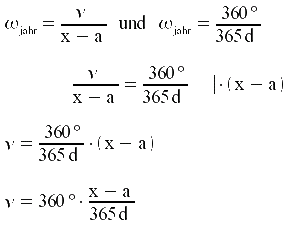4. Berechnung der astronomischen Sonnenscheindauer

4.1. Vorüberlegungen

Die astronomische Sonnenscheindauer bezeichnet die maximale Sonnenscheindauer eines Tages, die unter idealen Bedingungen möglich ist.

In der Fachlektüre wird bei der Berechnung der astronomischen Sonnenscheindauer meist auf die "Astronomischen Algorithmen" von Jean Meeus verwiesen, die auch bei kommerziellen Programmen zur Berechnung astronomischer Größen verwendet werden.

Für einen Laien sind diese Algorithmen aber kaum verständlich, da sie auf komplexen astronomischen Grundlagen aufbauen.

Die wesentlichen, für die Sonnenscheindauer verantwortlichen Begebenheiten, sind aber, in vereinfachter Form, jedem als die Entstehung der Jahreszeiten und Zustandekommen von Tag und Nacht bekannt.

Deshalb muss es mit diesen Kenntnissen auch möglich sein, eine vereinfachte, womöglich aber auch ungenaue, Berechnung durchzuführen.

4.2. Verwendete Grundlagen

Um mit der Kenntnis zur Entstehung der Jahreszeiten zu einem Ergebnis zu gelangen, sind viele Vereinfachungen und Annahmen nötig, auf die ich nun genauer eingehen werde. Diese nun folgenden Annahmen spiegeln wahrscheinlich den durchschnittlichen, stark vereinfachten Wissensstand eines Nicht-Astronomen wider und sind teilweise nicht korrekt! Außerdem sind die Jahreszeiten und Betrachtungen der Erde immer auf die nördliche Erdhalbkugel bezogen, um die Situation anschaulicher darstellen zu können.

Entstehung von Tag und Nacht

Ein Tag als Zeiteinheit dauert 24 Stunden und in dieser Zeitspanne dreht sich die Erde einmal um ihre eigene Achse, die durch die Pole geht. Da dabei immer nur eine Halbkugel der Erde von der Sonne beleuchtet wird, unterteilen sich die 24 Stunden in Tag (Sonnenschein) und Nacht (kein Sonnenschein). Das Verhältnis zwischen Tag und Nacht hängt von der Jahreszeit ab.

Entstehung der Jahreszeiten

Wie schon Galileo Galilei bewiesen hatte, dreht sich die Erde um die Sonne. Dies tut sie auf einer kreisförmigen Bahn. Die Umlaufdauer ist uns als ein Jahr bekannt, das im Kalender 365 Tage dauert. Die Ebene des Erdäquators ist allerdings nicht parallel zur gedachten Ebene der Kreisbahn (Ekliptik), sondern steht in einem konstanten Winkel von 23,5° dazu. Wenn man diese Ebene als Bezugspunkt nimmt, ist die Nordhalbkugel der Erde ein halbes Jahr lang der Sonne zugeneigt (Sommer) und ein halbes Jahr von der Sonne weggeneigt (Winter). Die verschiedenen Tageslängen und Jahreszeiten kommen folglich durch den unterschiedlichen Winkel (Deklination), in dem die Erde von der Sonne beleuchtet wird, zustande.

Anhang A 1: Graphische Darstellung der Jahreszeiten

Wichtige astronomische Zeitpunkte

In einem Jahr gibt es vier wichtige astronomische Zeitpunkte:

Datum im Jahr 2004	astronomische Bedeutung	meteorologische Bedeutung
20. März	Tagundnachtgleiche (Äquinoktium)	Frühlingsanfang
21. Juni	längster Tag des Jahres (Solstitium)	Sommeranfang
22. September	Tagundnachtgleiche (Äquinoktium)	Herbstanfang
21. Dezember	kürzester Tag des Jahres (Solstitium)	Winteranfang

Diese Zeitpunkte bestimmen auch die meteorologischen Jahreszeiten, aufgrund der verzögerten Erderwärmung, allerdings um ca. 1,5 Monate verzögert. Diese, für uns gewohnte, Einteilung in vier Jahreszeiten gilt allerdings nur für das Klima unserer Breitengrade.

Definition von Sonnenaufgang und Sonnenuntergang (Vereinfachung)

Aufgrund der großen Entfernung zwischen Sonne und Erde kann das Sonnenlicht als parallel angenommen werden.

Für die geplante stark vereinfachte Rechnung verwende ich folgende Definition von Sonnenaufgang und Sonnenuntergang: Die Sonne, die eigentlich als Scheibe am Horizont wahrgenommen wird, gilt dann als aufgegangen, wenn ihr Mittelpunkt den Horizont überschritten hat. Analog dazu der Sonnenuntergang.

Zusammenfassung der vorgenommenen Vereinfachungen:

• Die Erde ist eine Kugel und der Beobachter befindet sich direkt auf deren Oberfläche

• Die Schiefe der Ekliptik beträgt konstante 23,5°

• Vereinfachte Definition von Sonnenuntergang und Sonnenaufgang als 0° über dem Horizont

• Ein Tag dauert 24 h

• Ein Erdumlauf um die Sonne dauert 365 Tage

4.3. Sonnenscheindauer in Abhängigkeit der Deklination

Zweidimensionale Betrachtung von Tagundnachtgleiche und Solstitium für den 48. Breitengrad (Abb. 4-1)

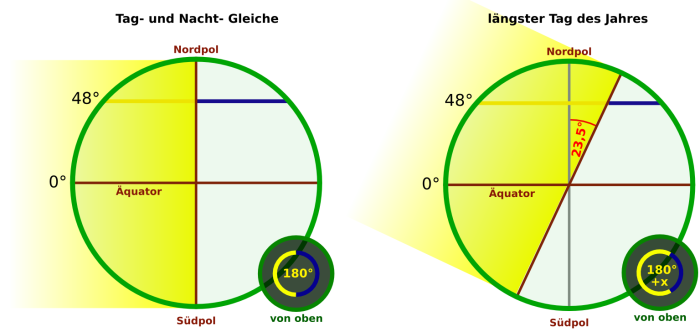
In der oberen Grafik werden zwei wichtige astronomische Zeitpunkte von der Seite betrachtet: Die Tagundnachtgleiche und der längste Tag des Jahres. Bei der Tagundnachtgleiche mit der Deklination 0° ist die Situation recht einfach, auch ohne Berechnung kann man erkennen, dass genau die Hälfte (180°) des 48. Breitengrades beleuchtet wird. Den beleuchteten Winkel auf dem Breitenkreis nenne ich Tagwinkel. Da dies einer halben Umdrehung um die Erdachse entspricht, beträgt die Sonnenscheindauer also 12 Stunden.

Beim längsten Tag des Jahres hat sich die Situation durch die positive Deklination verändert, so dass jetzt mehr als 180° beleuchtet werden. Dies ist in der Miniatur als 180° + x gekennzeichnet. Jetzt dauert der Tag also länger als 12 Stunden. Gesucht ist nun der Tagwinkel für diese Situation, da er das Verhältnis zwischen Tag und Nacht beschreiben kann.

Anhang A2: Dreidimensionale Darstellung des Verfahrens

Der daraus entstandene Rechenweg für die Sonnenscheindauer soll später bei bekannter Deklination auch auf alle anderen Tage angewendet werden können.

Da der gesuchte Tagwinkel μ aus einem 180° Winkel und zwei identischen zusätzlichen Teilen besteht, genügt es, den "Zusatzwinkel" zu berechnen. Dies kann theoretisch auf zwei Arten geschehen: Mit Hilfe der Sphärischen Trigonometrie oder auch mit elementarer Geometrie. Im Folgenden werde ich den Ansatz mit elementarer Geometrie beschreiben.

Definitionen und Deklarationen

α:="Deklination"
β:="geographische Breite"
δ:="Zusatzwinkel"
μ:="Tagwinkel"

Bei Betrachtungen der Erde verwende ich einen Einheitskreis, da die Maße unerheblich sind und nur ein Winkel gesucht ist.

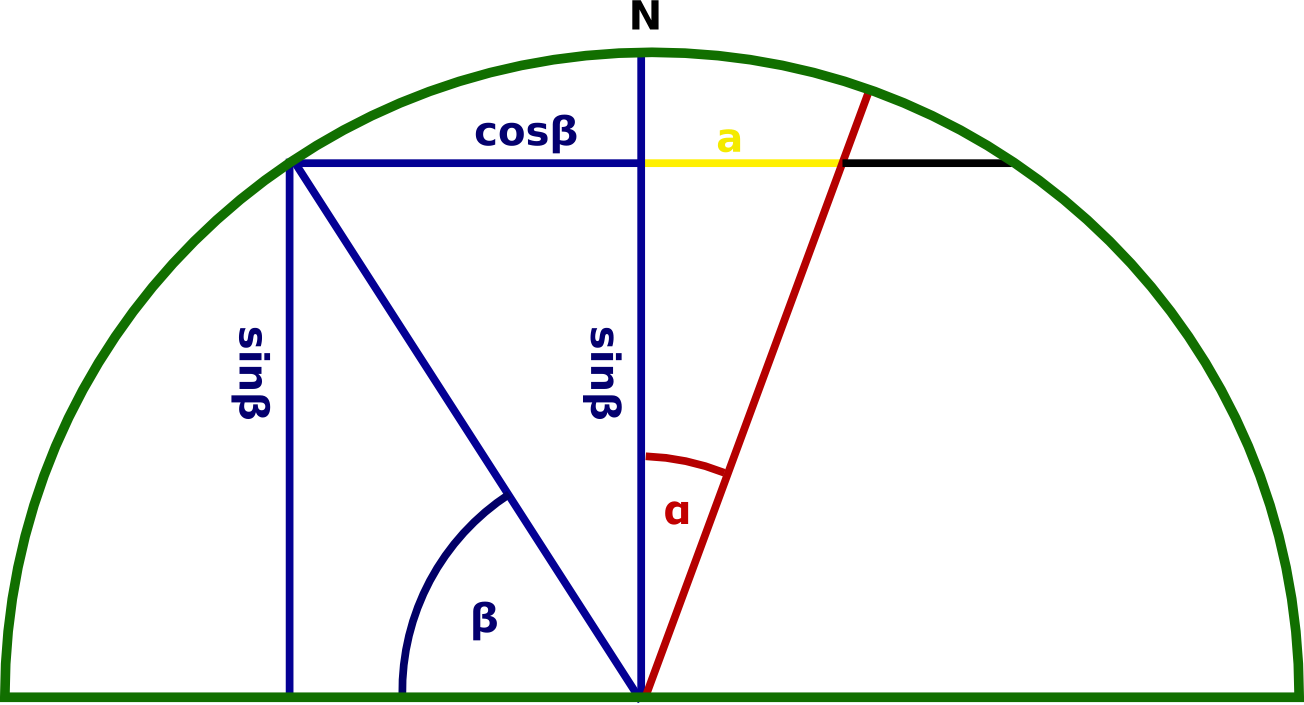
Schnitt durch die Erde - Berechnung des Abschnitts a

Bei bekannter Deklination kann der zusätzlich beleuchtete Abschnitt des Breitengrads berechnet werden. Der Abschnitt a, der hier berechnet wird, ist die Projektion des zusätzlich beleuchteten Winkels auf die Schnittfläche:

Abb. 4-2: Schnittebene ist die Ebene eines Längenkreises, der parallel zur Sonneneinstrahlung ist.

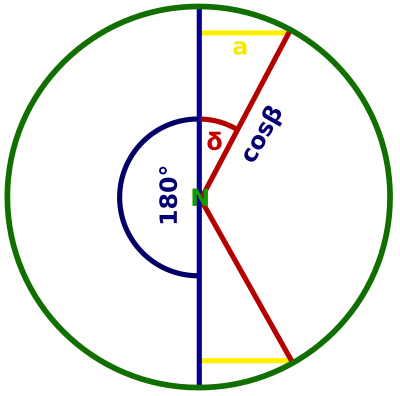
Breitenkreis - Umrechnung von a in einen Winkel (Abb. 4-3):

Abgebildet ist der Kleinkreis auf Höhe des gegebenen Breitengrads. Der Radius des Kleinkreises beträgt wie in der Zeichnung ersichtlich cos β.

Aus der Zeichnung folgt:

Bei gegebener Deklination und bekanntem Breitengrad kann also nun der beleuchtete Teil des Breitenkreises als Winkel berechnet werden.

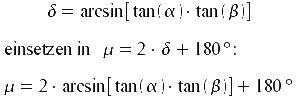
Rückführung auf die Tageslänge

Der berechnete Teil des Breitengrades muss nun, mit Hilfe der Erdrotation, in eine Zeiteinheit umgerechnet werden. Da bei meinem Rechenweg das Verhältnis zwischen Tag und Nacht berechnet wird, muss zur Berechnung der Tageslänge lediglich der Anteil des beleuchteten Breitengrads von 360°, mit 24 Stunden multipliziert werden.

Definitionsmenge

Einschränkung der Definitionsmenge aufgrund der Tangens:

Einschränkung der Definitionsmenge aufgrund des Arcussinus:

Für diese beiden Definitionslücken sollte sich eigentlich ein Zusatzwinkel ergeben, der im Betrag größer als 90° ist. Die Sonnenscheindauer kann aber nur Werte zwischen 0 und 24 einnehmen.

Es ist also eine Fallunterscheidung für die Sonnenscheindauer s(x) notwendig:

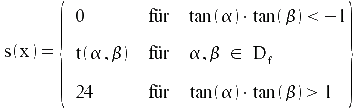
Mit dieser Formel kann man jetzt die theoretische Sonnenscheindauer für einen bestimmten Breitengrad berechnen, falls die Deklination bekannt ist.

4.4. Vorläufige Ergebnisse

Da aus der vorhergehenden Betrachtung der Jahreszeiten für vier Zeitpunkte im Jahr die Deklination festgelegt ist, soll mit diesen Werten die Tageslänge berechnet werden.

Beim Einsetzen der Werte in die vorher entstandene Formel ergeben sich folgende Werte:

Beispiel Wasserburg, geographische Breite β = 48°

Zeitpunkt	Deklination α	Tagwinkel δ	Sonnenscheindauer
Frühlingsanfang	0°	180°	12 h
Sommeranfang (längster Tag)	23,5°	237,8°	15,85 h
Herbstanfang	0°	180°	12 h
Winteranfang (kürzester Tag)	-23,5°	122,2°	8,15 h

Beispiel Oslo, geographische Breite β = 60°:

Zeitpunkt	Deklination α	Tagwinkel δ	Sonnenscheindauer
Frühlingsanfang	0°	180°	12 h
Sommeranfang (längster Tag)	23,5°	277,7°	18,51 h
Herbstanfang	0°	180°	12 h
Winteranfang (kürzester Tag)	-23,5°	82,3°	5,49 h

Beispiel Brasilia, geographische Breite β = -16°:

Zeitpunkt	Deklination α	Tagwinkel δ	Sonnenscheindauer
Frühlingsanfang	0°	180°	12 h
Sommeranfang (längster Tag)	23,5°	165,7°	11,05 h
Herbstanfang	0°	180°	12 h
Winteranfang (kürzester Tag)	-23,5°	194,3°	12,95 h

4.5. Berechnung der Deklination

Vereinfacht gesehen beschreibt die Erde eine Kreisbahn um die Sonne, mit der Umlaufzeit eines Jahres. Da die Äquatorialebene der Erde mit der Kreisbahnebene einen Winkel von 23,5 Grad einschließt, wird die Erde, wie bereits beschrieben, einmal von oben und einmal von unten beschienen, je nach Jahreszeit. Der Winkel zwischen den beiden Ebenen wird als "Schiefe der Ekliptik" bezeichnet. In den folgenden Berechnungen kommt er als ε vor.

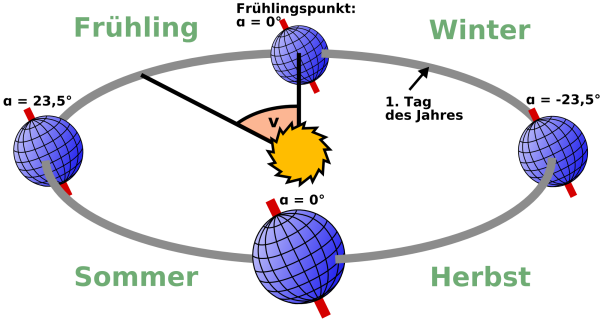
Der Verlauf zwischen den besagten -23,5° (-ε) und +23,5° (+ε) ist aufgrund der Kreisbahn eine harmonische Schwingung. Um den Sinus verwenden zu können, muss ein Positionswinkel der Erde auf dieser Kreisbahn definiert werden. Da die Deklination α im Frühlingspunkt 0° beträgt, setze ich diesen Zeitpunkt als 0° bzw. 360° des Positionswinkels, da der Sinus von 0° den Wert 0 ergibt.

Daraus entsteht eine Formel für die Deklination in Abhängigkeit des Positionswinkels ν:

Berechnung des Positionswinkels

Um den Positionswinkel für jeden Tag berechnen zu können, muss noch folgende Überlegung stattfinden:

Wenn die Erde sich 365 Tage vom Frühlingspunkt entfernt, läuft der Positionswinkel von 0° auf 360°. Die Winkelgeschwindigkeit beträgt also 360° in 365 Tagen:

Wenn man nun den Positionswinkel für einen bestimmten Tag sucht, muss man nur noch die Anzahl der vergangenen Tage nach dem Frühlingspunkt mit dieser Winkelgeschwindigkeit multiplizieren.

Wieviele Tage seit dem Frühlingspunkt vergangen sind, kann aus dem Kalender abgelesen werden. Um aber eine Berechnung für die Sonnenscheindauer im Jahresverlauf durchführen zu können, wird diese Überlegung in die Formel integriert.

Der Einfachheit halber werde ich die Zeitpunkte als natürliche Zahlen ("x-ter Tag des Jahres") angeben. Der Frühlingspunkt a war im Jahr 2004 der 80. Tag des Jahres.

Für den Positionswinkel des x.ten Tag im Jahr ergibt sich also folgende Gleichung:

(x - a) ist die Anzahl der vergangenen Tage seit dem Frühlingspunkt

Diese Gleichung für den Positionswinkel ν setzt man nun in die erste Gleichung für die Deklination ein:

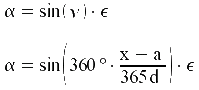
Bei dieser Gleichung für die Deklination ist jedoch zu beachten, dass nur mit ganzen Tagen gerechnet wird und sich deshalb Ungenauigkeiten ergeben können. Außerdem muss immer der passende Frühlingspunkt aus dem Kalender benutzt werden, da sich dieser jedes Jahr ändert. Für eine genauere Berechnung wäre der exakte Zeitpunkt des Frühlingspunktes notwendig, der explizit berechnet werden muss.

Einsetzen der Deklination in die Gleichung der Sonnenscheindauer

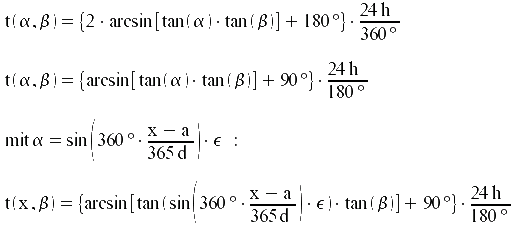
Die Fallunterscheidung aufgrund der Definitionslücken muss analog zur ausgeführten Fallunterscheidung s(x) getroffen werden!

Damit habe ich eine Gleichung erhalten, mit der ich für einen bestimmten Tag und eine bestimmte geographische Breite die Sonnenscheindauer berechnen kann. Voraussetzung dafür ist allerdings die Kenntnis der Schiefe der Ekliptik und der Frühlingspunkt.

4.6. Ergebnisse der gefundenen Formel

Beispiel Wasserburg

Um die Ergebnisse der erarbeiteten Formel überprüfen und darstellen zu können, habe ich sie mit der geographischen Breite von Wasserburg in ein Tabellenkalkulations-Programm eingesetzt:

β = 48°; a = 80; ε = 23,5°;

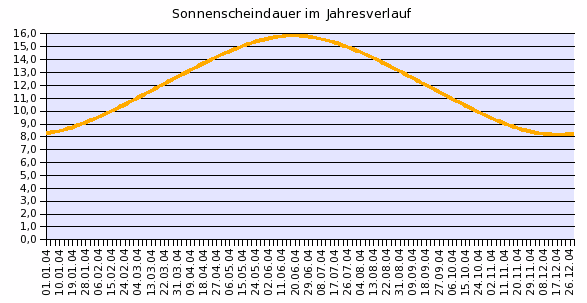
Es ergibt sich ein annähernd sinusförmiger Verlauf der Sonnenscheindauer, mit der vorher bereits berechneten Amplitude. Die Steigung ist jeweils am kürzesten und längsten Tag minimal.

Die subjektive Korrektheit der Formel soll nun anhand zweier Beispiele auch für andere Positionen auf der Erde überprüft werden:

Beispiel Island

β = 64°; a = 80; ε = 23,5°;

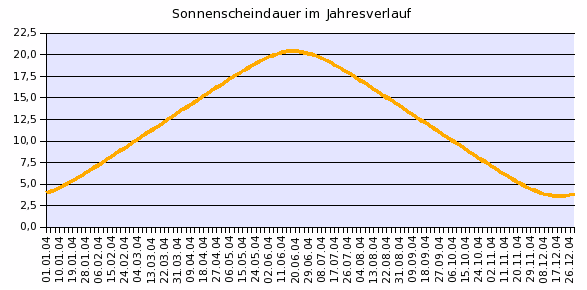
Neben einer beträchtlichen Amplitude von knapp 17 Stunden (20,41-3,59) zeigt sich ein nahezu linearer Verlauf der Sonnenscheindauer zwischen den Solstitien. Der sinusförmige Umschwung am längsten und kürzesten Tag ist mit einer hohen Krümmung versehen.

Beispiel Sydney

β = -34°; a = 80; ε = 23,5°;

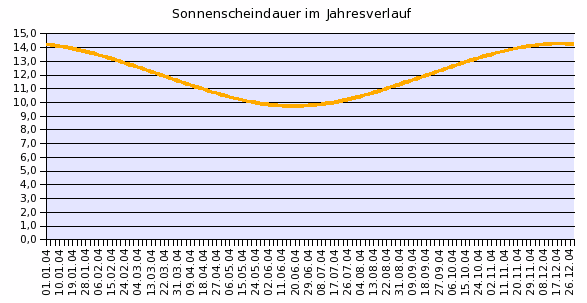
Wie erwartet zeigt sich auf der Südhalbkugel ein umgekehrtes Bild, der längste Tag des Jahres ist hier im Dezember. Ansonsten ist eine charakteristische Sinusform erkennbar, ähnlich wie beim Verlauf der Sonnenscheindauer in Wasserburg, lediglich mit einer geringeren Amplitude von ca. 4,5 Stunden.

4.7. Vergleich mit komplexen Berechnungsmethoden

Um meine vergleichsweise einfachen Berechnungen mit denen komplizierterer Art zu vergleichen, benutze ich geeignete Daten aus dem Internet als Referenz.

Auf der Internet-Seite des "Astronomical Applications Department"⁷ des "U.S. Naval Observatory" kann man nach der Eingabe seiner GPS-Koordinaten eine komplette Tabelle mit allen Sonnenaufgangs- und Sonnenuntergangszeiten für ein ganzes Jahr berechnen lassen. Das Rechenverfahren basiert auf den anerkannten "Astronomischen Algorithmen" von Jean Meeus.

Ich habe zum Vergleich mit meiner Berechnung die selben Parameter verwendet und die Aufgangs- und Untergangszeiten in die Sonnenscheindauer umgerechnet:

β = 48°

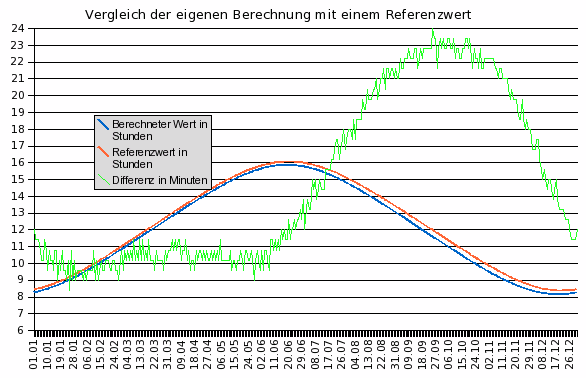
Die grüne Linie stellt die Differenz der beiden Graphen dar, zum besseren Ablesen in Minuten angegeben. Die Schwankungen der grünen Linie um +-1 Minute sind auf Rundungsfehler der Referenzwerte zurückzuführen, da diese Werte nur auf eine Minute genau angegeben waren.

Auf den ersten Blick ist erkennbar, dass der Graph meiner Funktion immer unterhalb des Referenz-Graphen bleibt. Die Abweichung (grüne Linie) bewegt sich im ersten Halbjahr relativ konstant bei 10 Minuten, im zweiten Halbjahr steigt sie jedoch bis auf ihr Maximum von 23 Minuten an. Insgesamt ergibt sich damit eine Standardabweichung von 15,6 Minuten.

4.8. Gründe für die Abweichung

Getrennte Betrachtung der Fehler

Bei der Suche nach den Gründen für die Abweichung, können die Fehler getrennt betrachtet werden:

Fehler 1: Die konstant zu niedrigen Werte.

Diese Abweichung muss aus der 1. Formel der Sonnenscheindauer bei bekannter Deklination entstanden sein, denn bei den Solstitien sind die Werte abweichend, obwohl dort die Deklination (-23,5 und +23,5) stimmt.

Fehler 2: Die Verschiebung auf der x-Achse und Abweichung im Verlauf

Dieser Fehler muss von der 2. Formel für die Deklination herrühren, da sie Startpunkt und Art des Verlaufs festlegt.

Definition von Sonnenaufgang und Sonnenuntergang

In der ersten Formel steckt eine große Vereinfachung, nämlich die Definition von Sonnenaufgang und Sonnenuntergang als 0° über dem Horizont.

Um die Unterschiede (Fehler 1) erklären zu können, betrachte ich zuerst die Definition von Sonnenaufgang und Sonnenuntergang der Referenz:

"For computational purposes, sunrise or sunset is defined to occur when the geometric zenith distance of center of the Sun is 90.8333 degrees."⁸

In dieser Berechnung gilt die Sonne also als aufgegangen, wenn sie 0,8333° unter dem Horizont steht. Dies wird durch folgende Faktoren begründet:

"The 50-arcminute geometric depression of the Sun's center used for the computations is obtained by adding the average apparent radius of the Sun (16 arcminutes) to the average amount of atmospheric refraction at the horizon (34 arcminutes)."⁹

Der Winkel von 50' kommt also zu einem Teil (16') durch die Größe der Sonne zustande, die als Scheibe wahrgenommen wird.

Wesentlich größeren Anteil (34') hat jedoch die Atmosphärische Brechung der Sonnenstrahlen. Ähnlich wie die Lichtbrechung durch das Wasser eines Sees, bricht die Atmosphäre der Erde das aus dem Vakuum eintreffende Sonnenlicht zur Erde hin. "[Ein] Stern, der scheinbar gerade untergeht, steht also in Wirklichkeit bereits über einen halben Grad unter dem Horizont"¹⁰. Einen Einfluss auf die Brechzahl der Erdatmosphäre hat die "vertikale Schichtung der Atmosphäre"¹¹, die "außerdem noch von Luftdruck und Lufttemperatur"¹² abhängt. Da dies schwer zu berechnen ist, wird allgemein bei Berechnungen (siehe Referenz) ein Mittelwert von 34' als Pauschalbetrag verwendet.

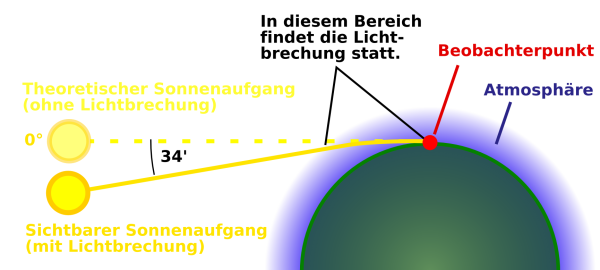
Wie in der vorherigen Grafik dargestellt, ist die Lichtbrechung in der Atmosphäre kein scharfer Knick, sondern eine Art "Biegung" der Sonnenstrahlen. Diese Sonderform der Brechung kommt zustande, da unsere Atmosphäre in hohen Schichten optisch dünner ist als in den erdnahen Schichten.

Die Definition von Sonnenaufgang und Sonnenuntergang, als 50' unter dem Horizont, hat also wahrscheinlich den Fehler 1 verursacht.

Schiefe der Ekliptik als mögliche Fehlerursache

Wie bei der Durchführung der Berechnung erwähnt, wurde bei der Schiefe der Ekliptik ein ungefährer Wert von 23,5° verwendet. Tatsächlich ist dieser Wert nicht einmal konstant. Die Erdachse rotiert nämlich nicht um eine raumfeste Achse, sondern sie führt zusätzlich sogenannte Präzessions- und Nutationsbewegungen aus, sie torkelt also wie ein Kreisel.

"Die Schiefe der Ekliptik beträgt derzeit 23.44 Grad. Sie ändert sich jedoch langperiodisch, weil kleine Gravitationseinflüsse aus dem Sonnensystem an der nicht ganz kugelförmigen Erde angreifen. Daher variiert ε innert 40.000 Jahren zwischen etwa 21°55' und 24°18'."¹³

Tabelle der Ekliptikschiefe -3000 bis +3000¹⁴

-3000  24°01.6'       0  23°41.7'      +1600  23°29.5'    
-2500  23°58.7'    +500  23°38.0'      +1700  23°28.7'
-2000  23°55.6'   +1000  23°34.1'      +1800  23°27.9'
-1500  23°52.4'   +1500  23°30.3'      +1900  23°27.1'
-1000  23°49.0'   +2000  23°26.4'      +2000  23°26.4'
- 500  23°45.4'   +2500  23°22.5'      +2100  23°25.6'
    0  23°41.7'   +3000  23°18.6'      +2200  23°24.8'

Für meine Berechnungen genügt trotz dieser Schwankungen ein konstanter Wert, da sie sich innerhalb kurzer Zeiträume abspielen. Dies ist also nicht für die Abweichungen verantwortlich. Trotzdem werde ich in allen nun folgenden Berechnungen einen genaueren aktuellen Wert (23,44°) verwenden, was zu einer marginal kleineren Amplitude der Sonnenscheindauer führen wird.

Deklination

Die Abweichungen im Verlauf der Sonnenscheindauer resultieren aus meiner stark vereinfachten Berechnung der Deklination. Hier kommt wahrscheinlich zum Tragen, dass die Erde keine ideale Kreisbahn beschreibt, sondern eine elliptische Bahn. Dies hat nämlich zur Folge, dass die Bahngeschwindigkeit nicht konstant ist. Im Winter, wenn die Erde der Sonne am nächsten ist, hat sie eine höhere Bahngeschwindigkeit als im Sommer, wenn sie den größten Abstand zur Sonne hat.

4.9. Optimierung der Berechnung

Neue Definition für die Formel der Sonnenscheindauer

Bei der Verbesserung meiner Berechnung geht es nun vor allem darum, die neue Definition für Sonnenauf- bzw. -untergang einzufügen, da dies die größte Abweichung von anderen Berechnungen verursacht hat. Dabei wird auch gleich der größte Nachteil meiner Berechnungsmethode deutlich, denn ich verwendete keine Kugelgeometrie, bei der man einfach die bekannten 0,833° zum Lauf der Sonne über dem Horizont hinzufügen könnte. Der Tagwinkel auf dem meine Berechnung basiert, ist ja lediglich der Mittelpunktswinkel eines Breitenkreises, bei dem dieser Korrekturwinkel dann in einem anderen Verhältnis eingehen muss.

Die neue Definition betrifft die zuallererst aufgestellte Überlegung, dass immer exakt eine Halbkugel der Erde beleuchtet wird. Dies ändert sich nun dahingehend, dass sich die Grenze zwischen Tag und Nacht um den sphärischen Abstand von 50' von der Sonne weg verschiebt:

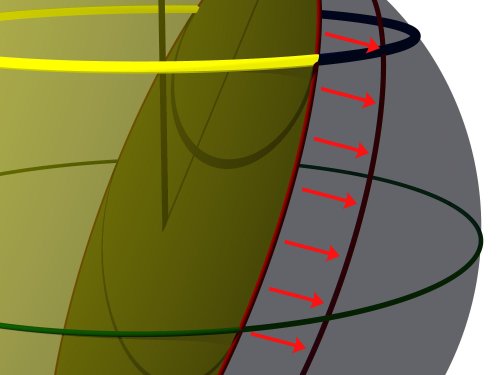
Damit ich mit dieser Information wieder auf die Sonnenscheindauer schließen kann, muss es möglich sein, den in der ersten Berechnung verwendeten Abschnitt a um das entsprechende Stück zu verlängern.

Projektion des sphärischen Abstand von 50' auf die Schnittebene

λ:="Definition von Sonnenaufgang/Sonnenuntergang"= 50'

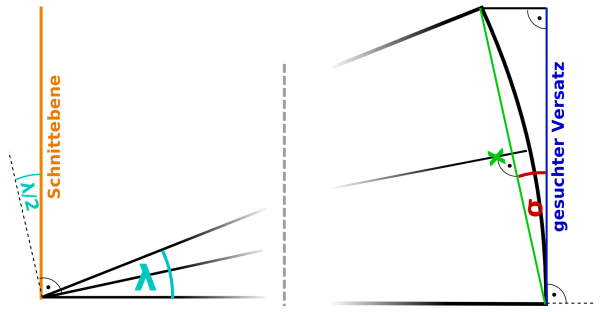
Aus der Zeichnung folgt für den Winkel σ:

Die Länge der Sehne x kann mit dem Winkel λ bestimmt werden:

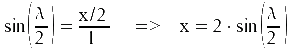
(Der Radius des Kreises beträgt 1)

Mit der Sehnenlänge x und σ kann der gesuchte Versatz v berechnet werden:

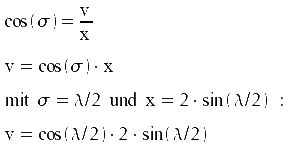
Dieser berechnete Abstand der beiden Ebenen, muss nun noch in die Richtung des Abschnitts a gebracht werden. Da dieser Versatz auf jedem Breitengrad der Erde gleich groß sein muss, habe ich ihn zum besseren Verständnis am Äquator eingezeichnet.

Aus der Zeichnung folgt der Zusatz z:

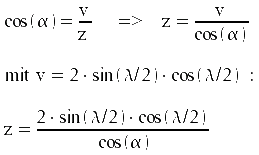
Berechnung des neuen Zusatzwinkels δ_neu, der Zusatz z verlängert dabei den Abschnitt a aus der alten Berechnung.

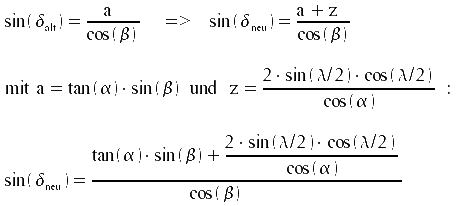
Rückführung von δ_neu auf den Tagwinkel μ_neu mit Hilfe der alten Berechnung

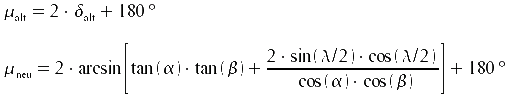
Einsetzen von μ_neu in die Formel der Sonnenscheindauer

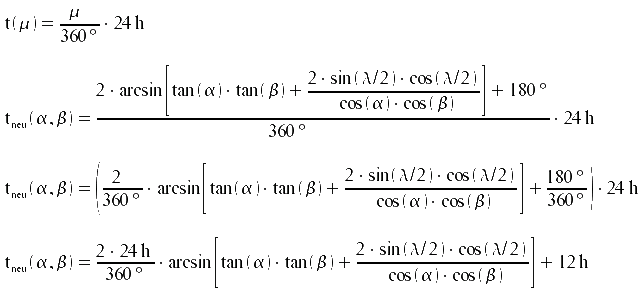
Die zur Fallunterscheidung führende Definitonsmenge gestaltet sich analog zur ersten Version der Formel!

In diese Formel muss nun lediglich bei α die Formel zur Deklination und bei λ der festgelegte Untergangswinkel von 50' eingesetzt werden. Zur besseren Übersichtlichkeit werde ich dies aber hier nicht durchführen, sondern erst in der Tabellenkalkulation.

4.10. Ergebnisse der optimierten Berechnung

Überprüfung der Formel der Sonnenscheindauer (Version 2)

Die quantitative Korrektheit dieser Ergebnisse soll nun unabhängig von den möglichen Fehlern der Deklinationsgleichung überprüft werden. Dazu verwende ich die Minima und Maxima der Deklination. Winkel ε ist bei der Berechnung Version 2 23,44°.

für β = 48°:

	eigene Berechnung (Version 1)	eigene Berechnung (Version 2)	Referenz (auf eine Minute genau)
längster Tag	15:51:00	16:02:46	16:03:00
kürzester Tag	08:09:00	08:22:01	08:22:00

Ein beliebig gewählter anderer Ort, hier β = -12°

	eigene Berechnung (Version 1)	eigene Berechnung (Version 2)	Referenz (auf eine Minute genau)
längster Tag	12:42:25	12:49:46	12:50:00
kürzester Tag	11:17:35	11:25:09	11:25:00

Bereits diese beiden Beispiele zeigen, dass die neue Definition von Sonnenaufgang und Sonnenuntergang zu einer Zunahme der Sonnenscheindauer um 7-15 Minuten führt. Im Vergleich mit der Referenz, die ja die selbe Definition verwendet, können nach Rundung identische Ergebnisse verzeichnet werden. Die Formel zur Sonnenscheindauer (Version 2) entspricht in ihren Ergebnissen offensichtlich denen anderer Berechnungen.

Ergebnisse der Berechnung (Version 2) im Jahresverlauf

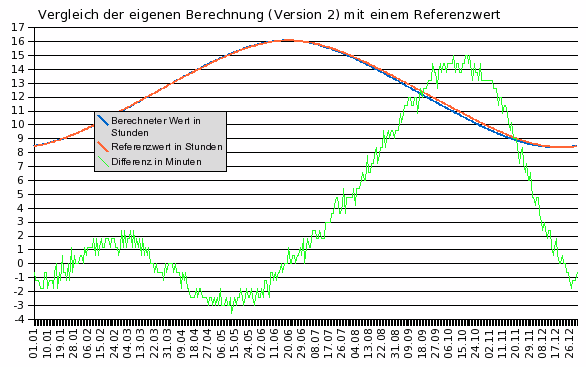
Der erneute Vergleich mit der Referenz zeigt ebenfalls signifikante Verbesserungen:

• Die neu berechnete Standardabweichung beträgt nur mehr 6,7 Minuten

• Im ersten Halbjahr liegen die Abweichungen bei ca. +- 2 Minuten

Trotzdem steigt die Abweichung zum Herbst stark an, meine Berechnung liegt Mitte Oktober um 15 Minuten unter der Referenz. Hier zeigt sich der Einfluss der ungenauen Berechnung der Deklination. Ab dem Sommer verändert sich die Deklination in Wahrheit etwas langsamer, da die Erde hier den größten Abstand zur Sonne hat und ihre Bahngeschwindigkeit infolge der 2. Keplerschen Regel geringer ist.

Für eine Tabelle der neuen Werte betrachten Sie bitte Anhang A 3

weiter zu Teil 5
zurück zur Übersicht